Become A Sponsor
|
Why Ads
How does it work?
-
The distance computer uses a mathematical function called the logarithm
to do multiplications.
-
A function is a "machine" that takes in a number and gives you back
a different number. For the same input number you always get the
same output number. Mathematicians call this a mapping.
-
The logarithm of a number x is written as log(x). This
function has a very special property. For any two positive numbers
a and b,
log(ab) = log(a) + log(b).
-
Remember that in algebra, ab means a times b.
So this means that the logarithm function turns a multiplication problem
into an addition problem. It is fairly easy to make physical objects
that perform addition, but much harder to make something that naturally
performs multiplication.
-
We can find an important property of the logarithm function very easily.
That is the value of log(1). Since 1a = a,
log(1a) = log(a) = log(1) + log(a).
-
The only way the last part can be true is if log(1) = 0.
-
Now, another important value is the number B such that log(B)
= 1. It turns out that we can choose B to be any positive
number greater than 1. Because our number system is based on 10,
it is convenient to choose B = 10. B is called the
base of the logarithm function, and the logarithm with base 10 is called
the common logarithm.
Now you can see how the distance computer is laid out.
-
We draw the scale by taking a set of numbers: 1.0, 1.1, 1.2, ...2.0, 2.5,
3.0,...10.0, and for each number x we make a mark at an angle of
360 log(x) degrees, and label this mark with the number x.
(Or, to be nearer the numbers we will actually encounter in using the distance
computer, we label the mark with the value 10x.)
Solving a step-distance problem.
-
The basic problem we need to solve is
D = NL,
-
where D is the total distance, N is the number of steps,
and L is the length of your step. Taking the logarithm of
this formula, we get
log(D) = log(N) + log(L)
-
If we draw the angles corresponding to log(D), log(N), and
log(L) on the distance computer, we see what is going on:
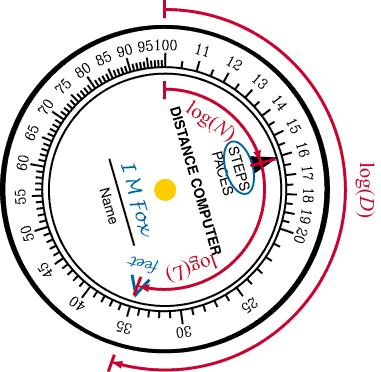
-
When we find the location of the "feet" mark, we are placing it 360 log(L)
degrees around from the "STEPS" marker.
-
When we rotate the computer so that "STEPS"
points to the number of steps, we have added in 360 log(N) degrees.
-
We now have log(D), which is turned back into D just by reading
the scale.
If you have enjoyed learning about the secrets of the distance computer,
think about taking more math courses in high school. The logarithm
function is usually studied in "Algebra 2." There are many other
wonderful things that you will learn in Geometry, Trigonometry, and even
Calculus. In Physics, Chemistry, and Biology, you will learn how
the mathematics works to produce the world around you. You have started
on a great adventure. Good luck!


|





